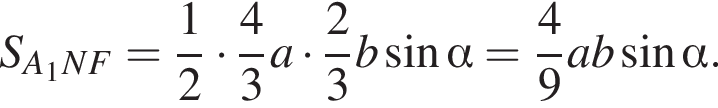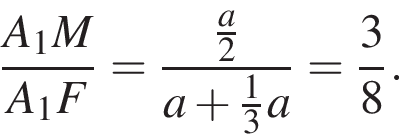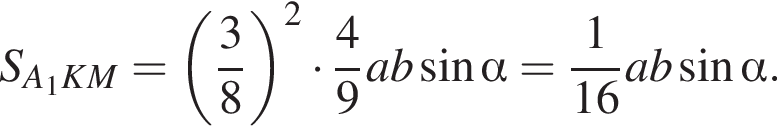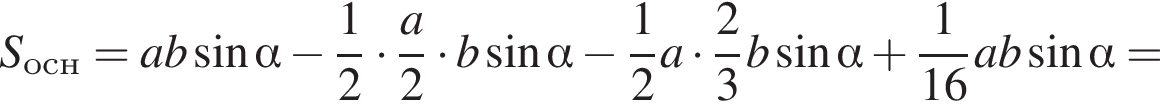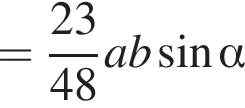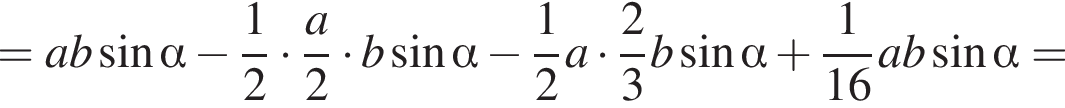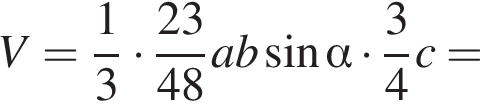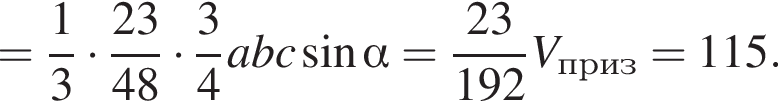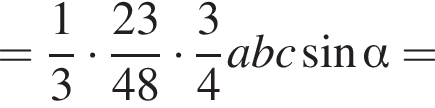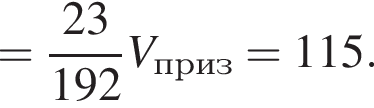i
ABCDA1B1C1D1 — прямая четырехугольная призма, объем которой равен 960. Основанием призмы является параллелограмм ABCD. Точки M и N принадлежат ребрам A1D1 и С1D1, так что A1M : A1D1 = 1 : 2, D1N : NC1 = 2 : 1. Отрезки A1N и B1M пересекаются в точке K. Найдите объем пирамиды SB1KNC1, если 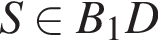 и B1S : SD = 3 : 1.
и B1S : SD = 3 : 1.

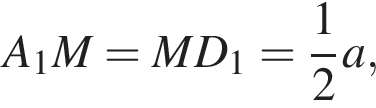
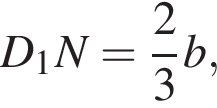
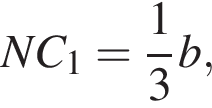
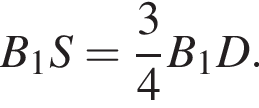
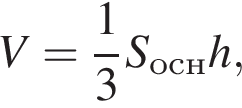 где основание — KNC1B1. Проведем высоту SE из точки S пирамиды SB1KNC1, как показано на втором рисунке.
где основание — KNC1B1. Проведем высоту SE из точки S пирамиды SB1KNC1, как показано на втором рисунке.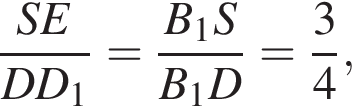 поэтому
поэтому 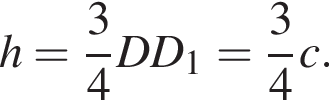



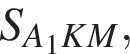 для этого сделаем дополнительное построение, проведя прямую параллельную B1M до пересечения с продолжением стороны A1D1 (см. рис. 3). Получившийся треугольник D1NF подобен треугольнику A1B1M по двум углам. Поэтому:
для этого сделаем дополнительное построение, проведя прямую параллельную B1M до пересечения с продолжением стороны A1D1 (см. рис. 3). Получившийся треугольник D1NF подобен треугольнику A1B1M по двум углам. Поэтому: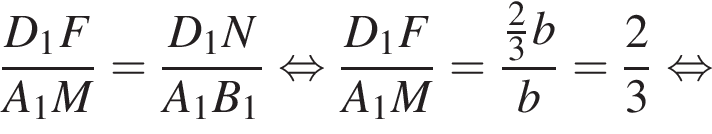
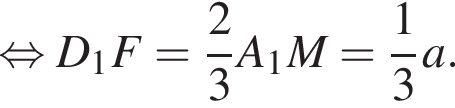

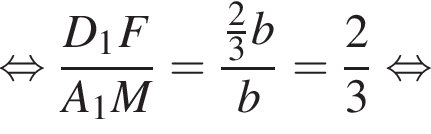
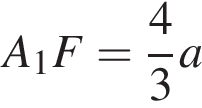 и
и 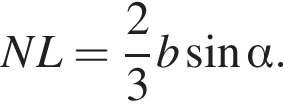 Соответственно, площадь треугольника A1NF равна
Соответственно, площадь треугольника A1NF равна